- Published on
わかりそうでわからない、けどちょっとわかる機械学習
- Authors

- Name
- Kikusan
機械学習の大枠がわかったので、ダンプする。
References
前処理
データの加工が一番大事。
いろいろやることはあるが、センスがいる。
- ラベリング : 量的・質的に分類
- クレンジング : 欠損値や外れ値、誤りデータを修正
- バランシング : データの偏りはないか
""" 欠損値を平均値で埋める"""
df.fillna(df.mean())
"""文字列を整形"""
def remove_html(data):
"""HTMLタグを削除"""
html_tag=re.compile(r'<.*?>')
data=html_tag.sub(r'',data)
return data
review_docs['review'] = review_docs['review'].apply(lambda z: remove_html(z))
"""カテゴリ変数をダミー変数にする"""
# age state point sex rank
# name
# Alice 24 NY 64 female 2
# Bob 42 CA 92 NaN 1
# Charlie 18 CA 70 male 1
# Dave 68 TX 70 male 0
# Ellen 24 CA 88 female 2
# Frank 30 NY 57 male 0
# drop_firstは多重共線性を防ぐ。maleとfemale二列あっても意味被ってしまうから。
pd.get_dummies(df, drop_first=True)
# age point rank state_NY state_TX sex_male
# name
# Alice 24 64 2 1 0 0
# Bob 42 92 1 0 0 0
# Charlie 18 70 1 0 0 1
# Dave 68 70 0 0 1 1
# Ellen 24 88 2 0 0 0
# Frank 30 57 0 1 0 1
モデル選定
こういう指標や,こういう表が一応用意されているが、実際経験が必要
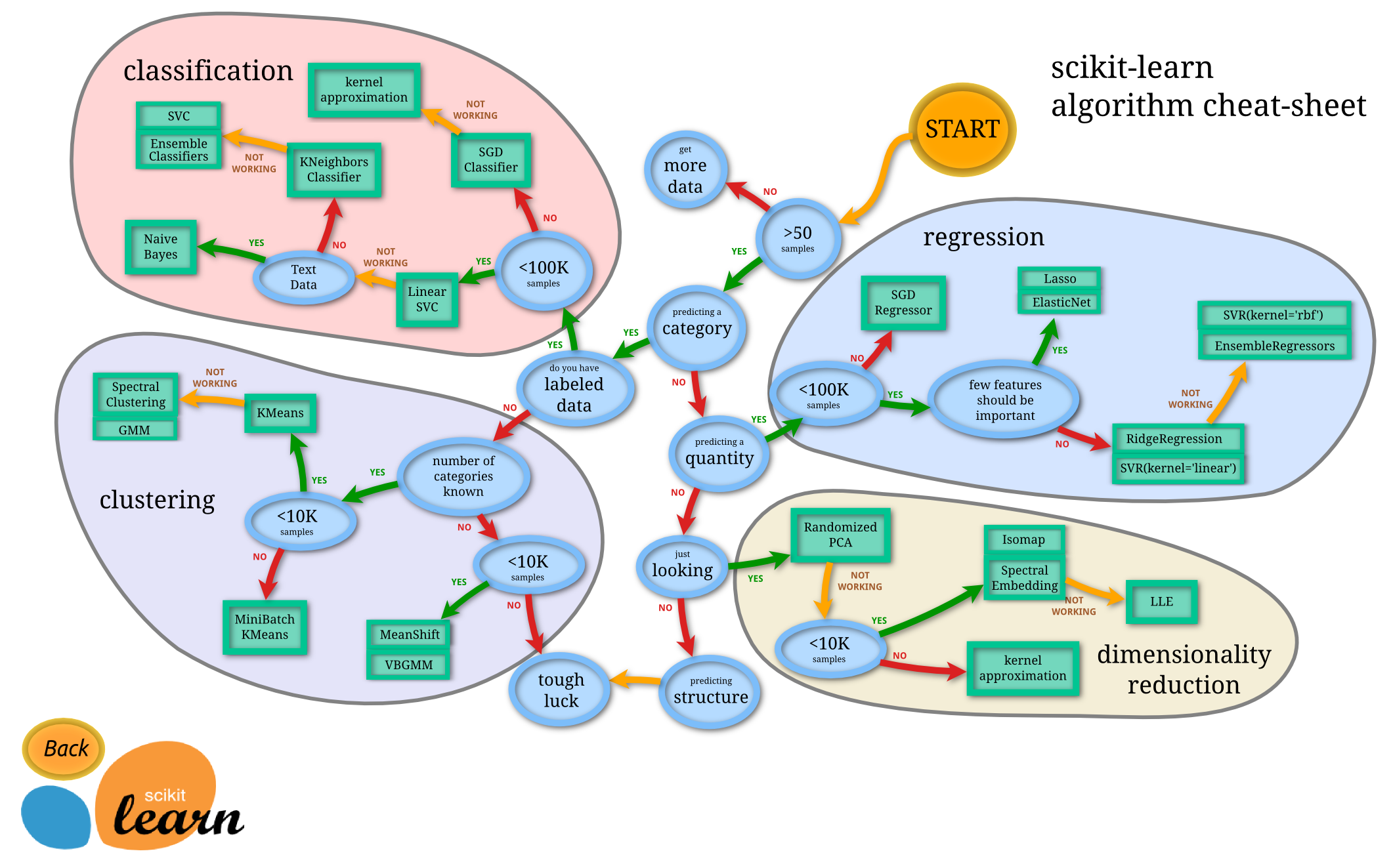
ハイパーパラメータチューニング
sklearnの引数のこと。モデルによって違う。
機械学習では損失関数(例えば最小二乗法)を最小化するように学習する。
- loss: 損失関数の種類
- C: 正則化の強さ
- penalty: 正則化項
※正則化は{損失関数\+正則化項(l1 or l2...)}を最小化するようにすることで過学習を防ぐ。ちなみに線形回帰で、l1を使うときラッソ回帰、l2を使うときリッジ回帰という。
GridSearchというので、良いパラメータも見つけてくれる。
from sklearn.linear_model import LogisticRegression as LR
from sklearn.model_selection import GridSearchCV # CVは交差検証するという意味 GridSearchもある
# {'パラメータ名': 試す値, ...}
grid = {'C': np.logspace(-3,3,7), 'solver': ['saga'], 'max_iter': [10000]}
model = LR()
gsc = GridSearchCV(model, grid, cv=4)
gsc.fit(X, y)
print(gsc.best_params_)
# {'C': 10.0, 'max_iter': 10000, 'solver': 'saga'}
学習
学習データとテストデータに分け、学習する
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
"""train_test_splitで分ける"""
d = train_test_split(X, y, test_size=0.25)
def run_classify(d, cl):
"""
d:(X_train, X_test, y_train, y_test)
cl:分類器インスタンス
"""
# 学習を行う
cl.fit(d[0], d[2])
# テストデータの分類(予測・推論)を行う
pred = cl.predict(d[1])
return pred
y_pred = run_classify(d, LR())
"""交差検証する(データをK個に分割してそのうち1つをテストデータに残りのK-1個を学習データとして正解率の評価を行う。時間かかるが精度↑)"""
def run_classify_cvp(X, y, cl):
"""
X: 説明変数
y: 目的変数
cl:分類器インスタンス
"""
# 交差検証で学習を行い、予測する 分割数=4
y_pred = cross_val_predict(cl, X, y, cv=4)
return y_pred
y_pred = run_classify_cvp(X, y, LR())
モデル評価
- 混同行列(Confusion matrix) : 分類したものの分布
正解
0 1
予測 0 OK[TP] 検出漏れ[FP]
1 誤判定[FN] OK[TN]
多クラス分類なら、クラス数×クラス数の行列になる。
- precision(TPR) : 正しいと予測したもののうち、正しいもの
- TP / TP + FP
- recall : 見つけるべきもののうち、正しく見つけられたもの
- TP / TP + FN
- F1 : 解答の分布が偏ったデータで見る指標 (0が9000 1が1000なら、全部0で予測すれば90%正解ジャン)
- TP/(TP + FP/2 + FN/2)
- accuracy : 正解率
- TP + TN / TP + FP + TN + FN
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
# (正解値, 予測値)
print('\nClassification report:\n', classification_report(y, y_pred))
print('Accuracy score: %.3f' % accuracy_score(y, y_pred))
print('\nConfusion matrix:\n',confusion_matrix(y, y_pred))
"""
Classification report:
precision recall f1-score support
0 0.90 0.88 0.89 6291
1 0.88 0.91 0.89 6209
accuracy 0.89 12500
macro avg 0.89 0.89 0.89 12500
weighted avg 0.89 0.89 0.89 12500
Accuracy score: 0.894
Confusion matrix:
[[5554 737]
[ 587 5622]]
"""
これは分類のものだが、回帰の場合は決定係数など、別の指標がある。